Binomial Distribution

FSbinomialinv(Trials, Probability, Optional Random Number)

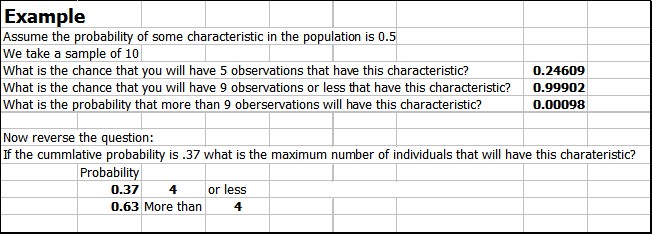
For ease of use and consistency there is a FinPak function for the inverse binomial that is consistent with other functions and expects as inputs the number trials, the probability of an event in the population and then an optional random probability number between 0 and 1 (Excel calls this the Criterion value). The Binomial is not a continuous distribution. It is defined only for discrete values, similar to the Poisson distribution. Look at the example for further explanation.

Table 1 shows the result of a simulation using FSbinomialinv for the values from the example. In this we got an outcome of 6 observations with characteristic. Table 2 shows the same simulation, but in this

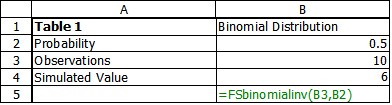
case the optional random number is supplied. In this case Rand() was used but another random number generator such as FSRandsq() could have been used.

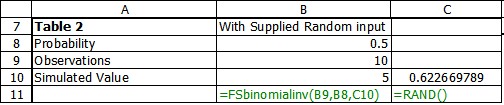
Table 3 computes the expect number of individuals (mean) and the standard deviation for the distribution that have the characteristics given the number of observations and the probability.

Figure 1 shows the Cumulative Distribution Function. This is figure is somewhat misleading given the discrete nature of the binomial distribution.

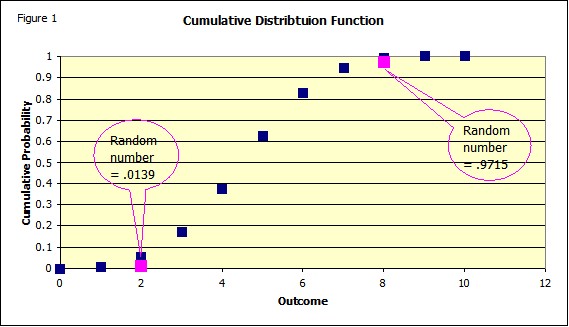
The eye wants to connect the points to get something that looks like Figure 1a perhaps.

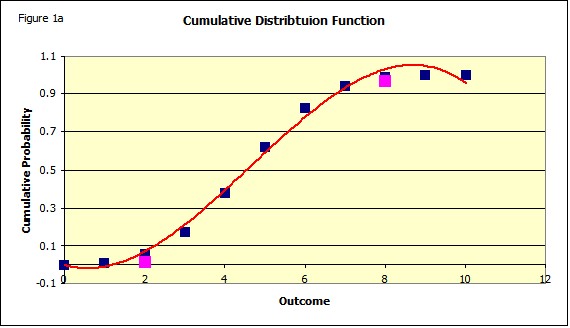
Which would be a "continuous" version of the binomial which does not exist. Figure 2 is a figure that more clearly shows the binomial distribution.

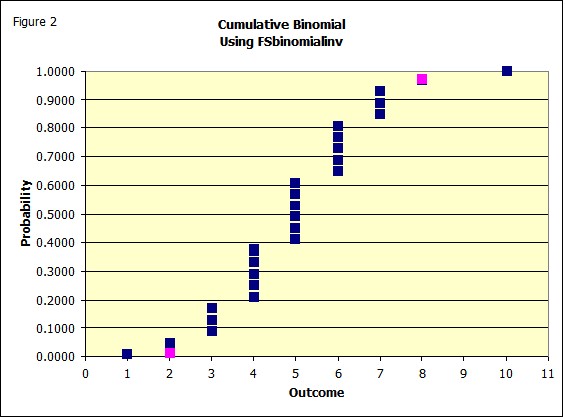
Notice that as the probabilities are "filled in" they produce vertical lines, not connected points. This is because of the discrete nature of the distribution which means you should really view this as a stair step function such as Figure 2a

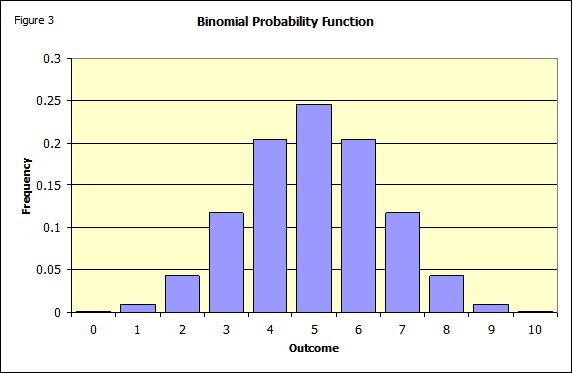
Figure 3 shows the distribution function for the Binomial Function for the data used in the example above. Notice that the distribution looks like the normal distribution, you could say that the binomial is a discrete version of the normal distribution.