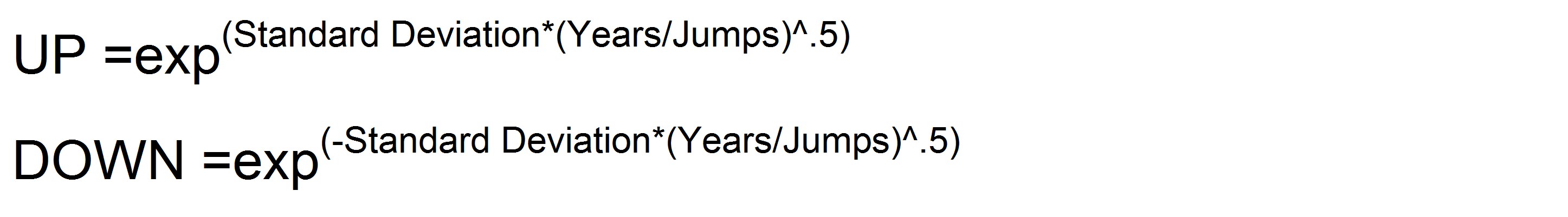
This function calculates an option value based on the Binomial Option Pricing Model. Like Black-Scholes it assumes a European Option. This function requires the user to supply the necessary inputs to the model. There is a companion function that labels the output. (BIYOPMTEXT). The function can be used as either an array function or a single cell function. If using it as an array formula highlight 7 cell (either column or row) click on the formula bar and type the formula, and then press Shift-Control-Enter Excel will supply the brackets around the formula. If it is used as a single cell formula the user can enter an optional value which returns a particular value for the option. The companion formula BIYOPMTEXT behaves the same way. It returns a label for the output from the BIYOPM function and is provided for convenience in labeling the output.
This function differs from BIOPM in that it allows the user to enter the data on an annual basis and the function will adjust data for the user. It also returns an estimate of the Standard Deviation that is implied in the UP and DOWN movements.
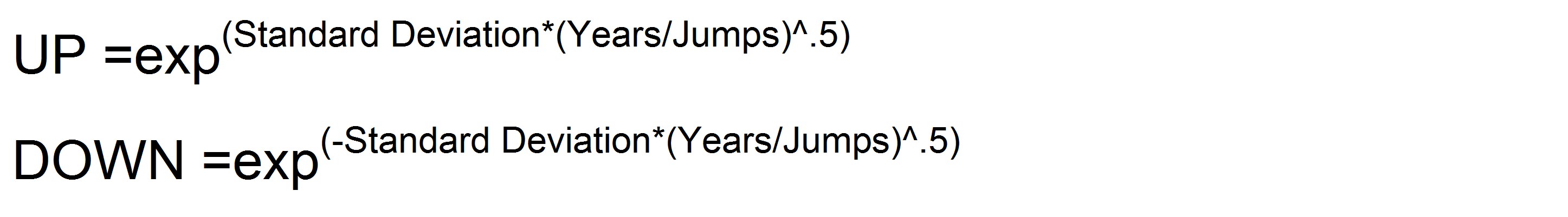
This function works back-wards, given the Up and Down movements it solves for the Standard Deviation. Since the Up and Down movements can be any number the user believes to accurate there is no requirement that the Standard Deviation estimates will be consistent. Hence the function returns both an Up Standard Deviation and a Down Standard Deviation. The computation mythology relies on the fact that state prices (Qu and Qd) are constant for any given interest rate ®, Up movement (U) and Down (D) movement. Thus the function computes the paths and multiples by the state prices to compute the payoffs in each state and then adds up the payoff to obtain the option value.
State prices can be computed by the following formulas:
Qu |
= ( R - D )/((1 + R )*( U - D )) |
Qd |
= ( U - R )/((1 + R )*( U - D )) |
The number of paths gets very large quickly. For 100 periods the number of possible paths is:
1,267,650,600,228,230,000,000,000,000,000
Fortunately the computations can be reasonable efficiently and routine is reasonably fast. However, you might want to consider this in your choice of parameters. In the example below the results using 4 years and 25 jumps returns essentially the same value for the option as BIOPM. Which is what we expect since the inputs are essentially the same? State prices can be computed by the following formulas:
Here are the inputs and form of the function: |
=BIYOPM(S,E,YEARS, JUMPS, UP,DOWN,R,OPTIONAL VALUE) |

For an understanding of Array Functions see Array Formulas

Copyright © 2009 Pieter Vandenberg